Critique of the 'Energy Resistance Principle' paper
DISCLAIMER: I'm a physicist with only a rudimentary understanding of biology. I recently started to get more seriously interested in the longevity field and the fight on aging (I attended LBF7). I'm reading a bunch of papers I find personally interesting. Note that any criticism below is not intended to belittle the work and may be a result of misunderstandings on my part.
Last week a friend of mine (https://x.com/TJThomps) sent me this paper titled 'The energy resistance principle'. He wanted to get my take on it as a physicist. I have since seen that both of the authors of the paper seem to be active on X (https://x.com/MitoPsychoBio, https://x.com/msahsorin) and are very enthusiastic about their work, which I appreciate. So I hope this article can be the start of a productive discussion about the ideas of the paper, which may very well contain some useful ideas. Clearing up misunderstandings will hopefully improve the work of the authors! In case you are not familiar with the paper, I recommend you read at least parts of it, because I won't be reiterating the ideas in detail. Let's get to it.
1. Overview of the ERP framework
I'll quickly try to summarize the main idea of the framework introduced in the paper.
The paper proposes that any biological system can be described by three scalar variables: the energy potential (), electron flux () and 'energy resistance' (). They borrow Joule's law to assert that and claim blends accumulation of energetic substrates and physiological demand for energy transformation (i.e. to perform work) and is treated as the rate of electron flux from food to oxygen. Supposedly, high yields hallmarks of aging and disease (via GDF15, inflammation and ISR), while low values of support adaption, sleep and recovery.
Figures 5-8 lay out how interventions (exercise, meditation, toxins, …) map onto changes in and and fig. 6 in particular describe the time evolution of how these variables relate to another based on a stimulation (exercise).
2. Summary of main problematic claims
For a very short tl;dr style overview, see the following table containing the major issues I see with the paper:
| Claim | What is required to make it scientific/useful |
|---|---|
| is a quantitative law. | Define EP and f with units + measurement recipes; show dimensional consistency. |
| ERP gives testable predictions across interventions. | Publish an estimator built from observables (EE, VO₂max, GDF15, …); preregister at least one discriminative prediction. |
| GDF15 is a practical eR marker. | Provide a calibration curve linking GDF15 and and show added predictive value beyond EE, VO₂max, BMI, age, …. |
3. Resistance, heat and work ATTACH
In the introduction of the paper, the authors introduce the Energy Resistance Principle (ERP) as being based on three assumptions. The first assumption is the following, which I'll quote verbatim:
(1) Life cannot exist without energy resistance. As in electrical systems where resistance is required for power dissipation (power law: ; if is zero, also is zero), resistance is required to transform different forms of energy into work and information (Figure 2). In wet biological systems, this transformation powers the molecular operations of life. Resistance regulates energy flux to ensure that energy is transformed into useful biological work rather than being entirely dissipated as heat, as in a burning flame.
I believe this assumption rests on a fundamental misunderstanding of physics and electrical circuits. What does the equation actually tell us from a perspective of physics? In an electrical circuit with resistance , if we have a current we produce dissipative losses of . The emphasis here is on losses. This is the energy we turn into heat without doing any useful work at all. While you may argue that the heat production is 'necessary' in order to do useful work as a byproduct, you may be partially right. But a) this is a practical engineering problem and more importantly b) you must not equate the amount of useful work done based on the amount of dissipative loss! If you do make that equation, you imply that more losses equals more work, which is false. Are your lamps at home LEDs or old school tungsten light bulbs? The "useful work" in the context of a lamp is the number of photons in energy ranges interesting for illumination it produces over time. It is not how large your energy bill is at the end of the month! For example, a tungsten bulb only uses about of its input energy to produce light while an LED requires only to produce the same amount of light.
In particular the last sentence explicitly shows the misunderstanding of the authors. Resistance is the source of heat dissipation. The lower the resistance is, the more energy you have to potentially do useful work.
So the statement that resistance is inherently needed to transform different forms of energy into work is simply false.
I think the misunderstanding relates to the fact that resistance in an electrical system is a well defined quantity that relates exactly to the heat loss one has. I expect the intuition the authors have is related to the fact that in realistic systems we always end up dealing with e.g. electrical resistance, friction, chemical processes producing waste heat etc. So it's easy to jump to the conclusion that the losses we have in practical systems equate to the amount of work we can do. From a purely physics standpoint, if you just consider a pendulum without friction, we have gravity performing work by pulling the pendulum downwards. We convert potential energy into kinetic energy and kinetic energy back into potential energy, i.e. we perform work.
To give a different example more related to electrical systems: if you were to build a system out of a perfect superconductor, you could build a computer that uses almost no energy. The 'almost' is because at some point (well beyond efficiencies of modern computers) you generally need to erase information (e.g. to clear registers or memory). Information itself is a physical thing and so you need energy to erase information. This is Landauer's principle and it is about per erased bit. Modern computers are a factor maybe 10 million away from that.
Figure 1 actually contains a rather interesting schematic that illustrates my point actually, fig. 1.
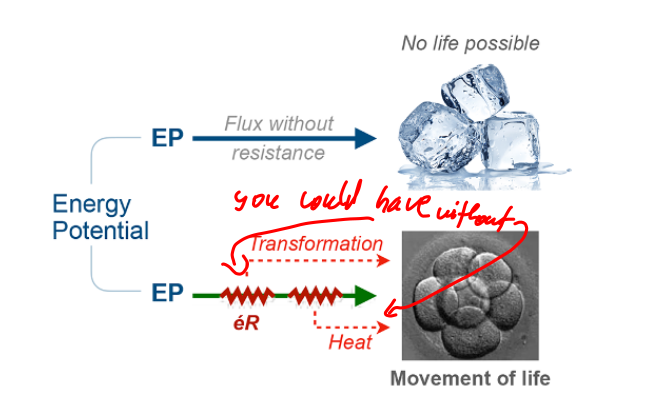
They quite literally show that the heat production and performance of useful work are two separate things in principle! You could do the useful work without heat losses in theory, indeed (in practice, who knows…).
Figure 4 of the paper includes this schematic explanation about the dissipative loss equation from above, fig. 2. It again seems to establish that the resistance is a requirement for the useful work performed.
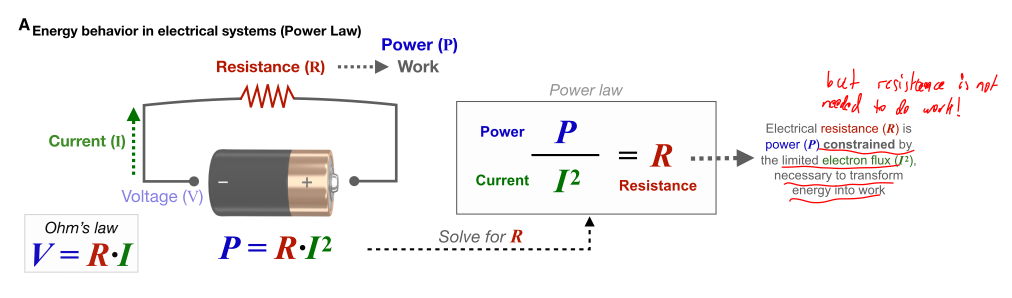
It's caption makes the same mistakes again, e.g.
In devices like electric motors, controlled resistance converts electrical energy into useful work, despite inevitable thermal energy loss.
While it is true that one could argue that the controlled resistance converts electrical energy into useful work, electrical engines actually produce very little thermal energy! The vast majority (over ) of the energy is directly converted to the kinetic / rotational energy the engine is supposed to produce. An ideal electrical engine could essentially achieve an efficiency of .
3.1. Resistance and warmth
Another (in my opinion as a non biologist) questionable statement is part of the caption of figure 1:
Energy resistance allows for transformation and dissipative energy loss, providing warmth and other required conditions for life (see Figure 2).
My understanding is that ectothermal animals like crocodiles receive the majority of their heat via the environment and not through metabolic processes producing heat as a byproduct. Therefore, the metabolism is not necessarily required to be used as a heat source.
For sure, from a physics point of view it is perfectly fine for a being to be entirely dependent on the environment to keep its operating temperature in a healthy range.
4. Resistors or transistors? ATTACH
Figure 3 contains a small explanatory schematic of an electrical circuit that biological systems are supposed to represent at a conceptual level (i.e. multiple resistances in series and parallel):
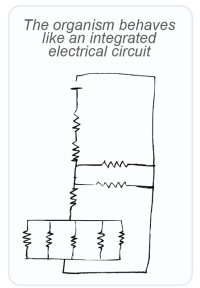
Up to this point in the paper, it was quite clear that the energy resistance principle was really talking about resistance. However, shortly after there is this section in the text referencing this schematic:
Using our electrical circuit analogy, the energetic cascade of life can be understood as a series of transistors, or variable resistances, connected to one another: some in series and some in parallel (Figure 3).
This again is worrying. A resistor and a transistor are two very different electrical components! A resistor is a passive electrical component with a fixed resistance, which dissipates energy as heat. A transistor on the other hand is an active component, which can modulate current flow (or in another sense modulate resistance). In terms of biology (both what is described in the paper and what seems sensible), a transistor is likely the more relevant comparison. However, the main equation of the model assumes a resistor-like behavior.
5. Voltage and power
Next up, when they introduce the three parts of their energy resistance equation, the 'energy potential' is introduced with the following statement:
For biology, the ERP proposes that EP subsumes both (1) the voltage-like accumulation of energetic substrates (e.g., glucose and lipids) and (2) the power-like physiological demand for energy transformation (e.g., physical work, in Watts or Joules). Analogous to voltage in electrical systems, EP provides the ‘‘push’’ for transformation, or the thermodynamic gradient for energy flux.
Again, this seems a gross misunderstanding of physics. Voltage and power represent two completely different physical quantities! One parameter cannot, by definition, capture the behavior of two different quantities.
To be specific, a voltage is given by
\[ [V] = \si{kg.m^2.s^{-3}.A^{-1}} \]
whereas power is given by:
\[ [W] = \si{kg.m^2.s^{-3}}. \]
They differ by a factor of , inverse electrical current. As such, they cannot both describe . This is before we even touch on biology at all.
6. Units and interactions
The paper states the following about ,
While this parallels Ohm’s law and the electrical power equation (\(P = R·I²\)), here, is a derived bioenergetic parameter with units analogous to resistance but emerging from dynamic biophysical constraints unique to living systems.
They relate to electrical resistance, but no explicit units are given. In multiple places the paper also talks about the eR being high or low in different parts of the body or as a result of different conditions. In the middle of the paper it even explicitly states the following:
EP can vary within minutes by 10–20 times at the whole-organism level and by over two orders of magnitude in muscle cells from rest to maximal contraction.
Again, neither before nor after did the paper ever even introduce what units any of these parameters are measured in, nor how one would even quantify any of these parameters in a more general sense. Everything is stated as qualitative relations, but somehow we pretend they are actually quantitative.
Due to the fact that no real definition is ever given, it's impossible to apply this equation to any tissue or biological system (or across different tissues).
6.1. Possible choices of units
The paper is clear that is a flux of electrons. Hence, it seems sensible to assume its units should be something like
\[ [f] = \si{s^{-1}} \]
possibly, electrons per second.
For the energy potential, the paper mentions that it should be related to the power demand of the system. So it seems reasonably to start with
\[ [\text{EP}] = \si{W}. \]
Putting this together, we arrive at units for of,
\[ \frac{[\text{EP}]}{[f²]} = \frac{\si{W}}{\si{s^{-2}}} = \frac{\si{J.s^{-1}}}{\si{s^{-2}}} = \si{J.s}, \]
which is action-like. At least for a "resistance" that is a rather bizarre unit.
Or maybe is actually unit less, because it just represents some flow as a dimensionless quantity. That puts the units to \([\text{eR}] = \si{W}\). But units of power for a resistance is again, not very sensible.
If the authors wish to be 'resistance-like', should be defined in a way that results in dimensions analogous to a resistance for . Alternatively, don't make the analogy to resistance!
We can summary the problem with the units as in tab. 1. This unit problem becomes critical later, when we evaluate the central equation of the ERP framework in sec. .
| Parameter | Claimed to be like | Should have units | Actual units (from EP/f²) | Problem |
|---|---|---|---|---|
| EP | "Voltage and power"? | W or V? | W or V? | Can't be both |
| f | Electron flux | s⁻¹ | s⁻¹ | Ok |
| eR | Resistance | Ω | J·s | Wrong! |
7. GDF15 and high
The closest explicit reference to any biological system that could very loosely be seen as relating the equation to something one can measure, is the mention of GDF15 levels as a marker for . This is used in many places throughout the paper. However, the paper ends up concluding that measuring GDF15 levels gives us an insight into . Yet, the relation is never more than hypothesized.
The introduction of GDF15 as a marker is here (subsection markers):
The best available marker in humans is the secreted cytokine GDF15, a member of the transforming growth factor β (TGF-β) family.
To be specific:
- it is unclear whether GDF15 is caused by high or merely correlated with it,
- quantitative relationship between GDF15 and and how to use GDF15 measurements to actually calculate values,
- whether GDF15 reacts to all / can distinguish between different mechanism leading to elevated .
To my (limited) understanding, GDF15 levels can rise as a result of many different factors. It seems to represent a result of various stressors. Therefore, it is difficult to view it as a general marker for .
8.
Last, but certainly not least, let's talk about the equation proposed as the fundamental mechanism for the energy resistance principle,
\[ \frac{\text{EP}}{f²} = \text{eR} \]
This is a scalar equation. It relates three parameters to another. It does not say anything about dynamics. If this equation holds, it follows that
\[ \frac{∂\text{eR}}{∂\text{EP}} = \frac{1}{f²} \]
and
\[ \frac{∂\text{eR}}{∂f} = -\frac{2\text{EP}}{f³}. \]
Both are simple power law relations! Yet the paper paper states explicitly,
As proposed in our initial formula, scales linearly with but exponentially with , a relation that predicts that organisms can accommodate relatively large fluctuations in EP on the scale of seconds to hours via relatively small changes in flux.
and
Consequently, changes in f are expected to produce an exponential effect on compared with linear changes in .
The term 'exponential' has a well defined meaning in mathematics. It is reserved for the exponential function, . I get the impression that this imprecise language implies less than ideal understanding of mathematics. As a result I imagine the relationship was probably chosen, because it appears to be the simplest way to achieve non-linear behavior.
By being such a scalar equation, it literally means one intervention that, say, increases can be counteracted by another mechanism that lowers or increases (more on that below).
Further, it is entirely unclear why the relation would even really be just and not any other relation. They mention:
the squaring of flux () reflects the nonlinear dynamics of biological energy transformations,
This is not a justification or derivation as to why should be correct. Sure, biology has nonlinear dynamics, but it would be naive to assume that they should just be .
8.1. Processes influencing , , ATTACH
Section summary: The ERP, as written in the paper, is an algebraic identity. Fig. 6 (below) implies a coupled, dynamic system.
Now we get to the most problematic part of the framework presented in the paper. Feel free to ignore my annotations. First figure 5 presents which processes / interventions affect which parameter, fig. 4.
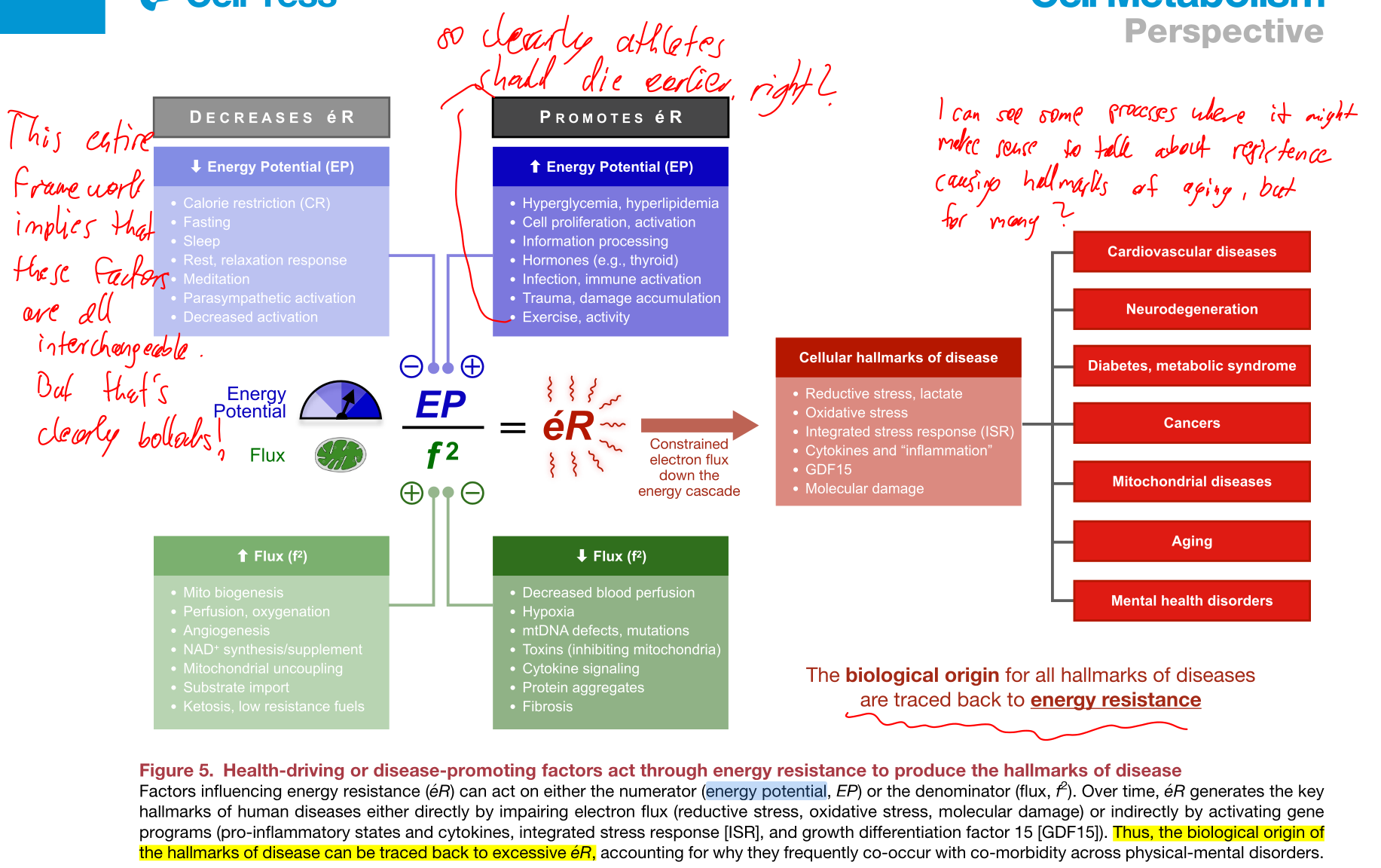
Next up, we have figure 6, fig. 5.

Now, what is the fundamental problem here?
There are two major problems stemming from the fact that the framework is based on a single scalar equation: .
- In this framework, different processes, interventions or conditions affect one of the three variables. This means that an increase in one aspect affecting a parameter can be directly offset by something completely unrelated. Say, DNA mutations mentioned as decreasing the flux can simply be offset by meditating a squared amount more! A biological system simply contains too many coupled systems to be able to express their relationship via a single scalar equation. The equation as it is simply makes wrong statements about biology.
- Figure 6 includes the schematic of how exercise affects , and at different timescales. The problem is that the equation has absolutely no dynamic component. This equation cannot express dynamical changes as presented here. We need (likely multiple coupled) differential equations to model how different parameters change over time and an explicit time dependence of the parameters in the first place.
To be more explicit, fig. 6 in the paper shows parameters overshooting, recovering and long drifts over timescales of a week. Yet, the scalar equation has no way to model a time dependence and thus the shown curves cannot be the related to the ERP equation.
Given that the entire framework rests on this one equation, I'd argue that as explained in this paper, the framework is fundamentally incomplete or broken.
9. A quantitative framework?
Initial evidence relating GDF15 to fatigue and psychosocial factors,119,144 as well as brain reductive stress (elevated NADH/NAD+) in schizophrenia and bipolar disorder,145 supports this contention, calling for more research grounded into a quantitative energetic framework [emphasis mine] like the ERP.
Unfortunately, the entire paper does not give me the sense that ERP at this time is in any way an actual quantitative framework. It is entirely qualitative. There is no way to calculate anything with the presented equation.
This kind of stuff:
These include transcranial magnetic stimulation; meditation, breathwork, and other contemplative practices; the use of psychedelic substances cryotherapy; acupuncture; and photobiomodulation, among others. Rather than acting molecularly—like conventional pharmacotherapy—could these approaches operate by modulating eR directly? The ERP provides a quantitative framework to begin testing this possibility.
makes it seem like they are completely convinced this framework actually offers something useful in a quantitative sense. I'm worried that this is just confirmation bias.
9.1. Towards a quantified relation
In order to turn this into a falsifiable, quantitative marker, we would at least expect some kind of quantitative relation between and GDF15 levels.
If we identify GDF15 as a marker for and map the energy expenditure (EE) of the system to the energy potential and finally, for example, VO2max to the flux capacity, , we could write down a predictor of the form:
\[ \text{E}[\text{eR}] = α·\text{GDF15} + β·\text{EE} + γ·(\text{VO}_2\text{max})^{-1}. \]
Here the inverse VO2max represents the fact that a higher flux capacity should relate to a lower (see fig. 5).
This is just an example, but it would allow us to actually fit a model based on observed data to compute an actual value. In reality the relation would certainly be more complicated as other factors would need to be included and the powers may not be correct on each term etc. Such an approach would just be a minimum example to talk about a quantitative framework.
10. Sketch of a dynamic model for ERP
The following is just a basic sketch, but it illustrates the pieces that are missing (or would be needed) in order to allow the ERP to account for things like the exercise adaptations mentioned in fig. 6. Below for now we ignore the issue of problematic units that we mentioned in sec. Possible choices of units for the time.
We have three state variables, which must be time dependent:
- : effective energy pressure, \([\text{EP}] = \si{W}\) or similar
- : electron flux capacity,
- : defined by (a heuristic 'burden' index)
Now we'd need some kind of coupled dynamics, i.e. how do these change over time and interact with another?
\begin{aligned} \frac{\mathrm{d}\text{EP}}{\mathrm{d}t} &= I(t) − κ_d·\text{EP} - κ_{\text{EP}}·u_{\text{EP}}(t) & \text{inputs minus dissipation minus control} \\ \frac{\mathrm{d}f}{\mathrm{d}t} &= β_R·R(t) - β_d·D(t) + κ_f·u_f(t) & \text{repair signals minus damage plus training/therapy} \\ y(t) &= α·\text{GDF15}(t) + β·\text{EE}(t) + γ·(\text{VO}_2\text{max}(t))⁻¹ & \text{observable estimator } E[\text{eR}] \\ \end{aligned}Here we introduced a few more variables:
- : damage accumulated over time,
- : repair signals, increasing flux capacity over long time scales,
- and : control parameters for energy potential or flux, respectively. Represented by interventions like exercise, sleep etc.,
- : any input that raises .
Negative terms decrease the parameters and positive ones increase them. The coefficients, in the first two equations are intended to be positive.
This would give a starting point to analyze the framework in a quantitative sense, derive solutions to these equations and make predictions about how different interventions affect the system.
11. Peer review quality
Finally, even though it may be minor, with the criticism of the previous sections it raises red flags. A small excerpt of the caption of fig. 1 is shown in 6.

Now, a duplicate "and and" is not a real issue, but it makes me question with how much detail the peer review process for this paper was performed in the first place, as these things seem very obvious (but that may just be me). At least it raises some questions about the peer review process, at least in Cell Metabolism. The presented unit incompatibilities and mathematical errors (e.g. exponential vs power law, scalar equation for dynamics) should have been caught during review.
In particular for work that is interdisciplinary, a journal should ensure to have a panel of reviewers who can verify claims of all disciplines.
12. Conclusion
The ERP paper might have some interesting ideas and for biologist's there may well be a lot to be excited about. I assume from a biologists perspective the ideas of the ERP framework might be exciting, applicable and useful. However, its embedding into physics is questionable at the moment.
The above represents the most important points I wanted to raise about it. There were other things I marked in the paper, but this article would look even more like I'm just criticizing for the sake of it. I hope this was useful and did not come across as too confrontational.